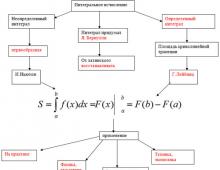
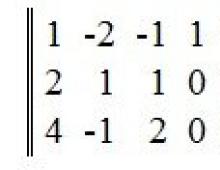
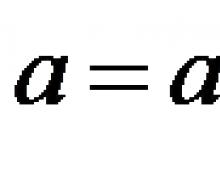Juhusliku suuruse x määrab funktsioon. Pideva juhusliku suuruse arvulised karakteristikud

Nagu teada, juhuslik muutuja nimetatakse muutuvaks suuruseks, mis võib olenevalt juhtumist omandada teatud väärtused. Juhuslikud muutujad on tähistatud ladina tähestiku suurtähtedega (X, Y, Z) ja nende väärtused on tähistatud vastavate väiketähtedega (x, y, z). Juhuslikud muutujad jagunevad katkendlikeks (diskreetseteks) ja pidevateks.

Diskreetne juhuslik suurus on juhuslik muutuja, mis võtab teatud nullist erineva tõenäosusega ainult lõpliku või lõpmatu (loendatava) väärtuste komplekti.

Diskreetse juhusliku suuruse jaotusseadus on funktsioon, mis ühendab juhusliku suuruse väärtused neile vastavate tõenäosustega. Jaotusseadust saab täpsustada ühel järgmistest viisidest.

1 . Jaotusseaduse saab esitada tabeli abil:

kus λ>0, k = 0, 1, 2, … .

V) kasutades jaotusfunktsioonid F(x) , mis määrab iga väärtuse x puhul tõenäosuse, et juhuslik suurus X võtab väärtuse, mis on väiksem kui x, s.t. F(x) = P(X< x).

Funktsiooni F(x) omadused

3 . Jaotusseadust saab graafiliselt täpsustada – jaotuspolügoon (polügon) (vt ülesanne 3).

Pange tähele, et mõne probleemi lahendamiseks pole vaja teada jaotusseadust. Mõnel juhul piisab ühe või mitme arvu teadmisest, mis kajastavad jaotusseaduse kõige olulisemaid tunnuseid. See võib olla arv, millel on juhusliku suuruse "keskmine väärtus", või arv, mis näitab juhusliku suuruse keskmist kõrvalekalde suurust selle keskmisest väärtusest. Selliseid numbreid nimetatakse juhusliku suuruse arvulisteks tunnusteks.

Diskreetse juhusliku suuruse põhilised numbrilised karakteristikud :

• Matemaatiline ootus diskreetse juhusliku suuruse (keskmine väärtus). M(X)=Σ x i p i.
  Binoomjaotuse korral M(X)=np, Poissoni jaotuse korral M(X)=λ
• Dispersioon diskreetne juhuslik suurus D(X) = M2 või D(X) = M(X 2) − 2. Erinevust X–M(X) nimetatakse juhusliku suuruse kõrvalekaldeks tema matemaatilisest ootusest.
  Binoomjaotuse korral D(X)=npq, Poissoni jaotuse korral D(X)=λ
• Standardhälve (standardhälve) σ(X)=√D(X).

Näiteid ülesannete lahendamisest teemal “Diskreetse juhusliku suuruse jaotuse seadus”

Ülesanne 1.

Välja anti 1000 loteriipiletit: neist 5 võidab 500 rubla, 10 võidab 100 rubla, 20 võidab 50 rubla, 50 võidab 10 rubla. Määrata juhusliku suuruse X – võidud pileti kohta – tõenäosusjaotuse seadus.

Lahendus. Vastavalt ülesande tingimustele on võimalikud järgmised juhusliku suuruse X väärtused: 0, 10, 50, 100 ja 500.

Ilma võiduta piletite arv on 1000 – (5+10+20+50) = 915, siis P(X=0) = 915/1000 = 0,915.

Samamoodi leiame kõik muud tõenäosused: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X) =500) = 5/1000=0,005. Esitame saadud seaduse tabeli kujul:

Leiame väärtuse X matemaatilise ootuse: M(X) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5

3. ülesanne.

Seade koosneb kolmest iseseisvalt töötavast elemendist. Iga elemendi ebaõnnestumise tõenäosus ühes katses on 0,1. Koostage jaotusseadus ebaõnnestunud elementide arvu kohta ühes katses, konstrueerige jaotuspolügoon. Leia jaotusfunktsioon F(x) ja joonistada see. Leidke diskreetse juhusliku suuruse matemaatiline ootus, dispersioon ja standardhälve.

Lahendus. 1. Diskreetsel juhuslikul muutujal X = (ebaõnnestunud elementide arv ühes katses) on järgmised võimalikud väärtused: x 1 = 0 (ükski seadme elementidest ei ebaõnnestunud), x 2 = 1 (üks element ebaõnnestus), x 3 = 2 ( kaks elementi ebaõnnestusid ) ja x 4 =3 (kolm elementi ebaõnnestus).

Elementide rikked on üksteisest sõltumatud, iga elemendi rikke tõenäosus on võrdne, seetõttu on see rakendatav Bernoulli valem . Arvestades, et tingimuse järgi n=3, p=0,1, q=1-p=0,9, määrame väärtuste tõenäosused:
P 3 (0) = C 3 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P 3 (1) = C 3 1 p 1 q 3-1 = 3 * 0,1 * 0,9 2 = 0,243;
P 3 (2) = C 3 2 p 2 q 3-2 = 3 * 0,1 2 * 0,9 = 0,027;
P 3 (3) = C 3 3 p 3 q 3-3 = p 3 = 0,1 3 = 0,001;
Kontrollige: ∑p i = 0,729+0,243+0,027+0,001=1.

Seega on soovitud X-i binoomjaotuse seadus järgmine:

Joonistame x i võimalikud väärtused piki abstsisstellge ja vastavad tõenäosused p i piki ordinaattelge. Konstrueerime punktid M 1 (0; 0,729), M 2 (1; 0,243), M 3 (2; 0,027), M 4 (3; 0,001). Ühendades need punktid sirgjooneliste segmentidega, saame soovitud jaotuspolügooni.

3. Leiame jaotusfunktsiooni F(x) = Р(Х

Kui x ≤ 0 on meil F(x) = Р(Х<0) = 0;
0 eest< x ≤1 имеем F(x) = Р(Х<1) = Р(Х = 0) = 0,729;
1 eest< x ≤ 2 F(x) = Р(Х<2) = Р(Х=0) + Р(Х=1) =0,729+ 0,243 = 0,972;
2 jaoks< x ≤ 3 F(x) = Р(Х<3) = Р(Х = 0) + Р(Х = 1) + Р(Х = 2) = 0,972+0,027 = 0,999;
x > 3 korral on F(x) = 1, sest üritus on usaldusväärne.

Funktsiooni F(x) graafik

4. Binoomjaotuse X jaoks:
- matemaatiline ootus M(X) = np = 3*0,1 = 0,3;
- dispersioon D(X) = npq = 3*0,1*0,9 = 0,27;
- standardhälve σ(X) = √D(X) = √0,27 ≈ 0,52.

Matemaatiline ootus diskreetset juhuslikku muutujat nimetatakse:

Lõpmatu väärtuste hulga korral on jada (4.4) paremal küljel ja me võtame arvesse ainult neid X väärtusi, mille jaoks see jada on absoluutselt konvergentne.

M(X) tähistab juhusliku suuruse keskmist eeldatavat väärtust. Sellel on järgmised omadused:

1) M(C)=C, kus C=konst

2) M (CX) = CM (X) (4,5)

3) M (X+Y)=M(X)+M(Y), mis tahes X ja Y korral.

4) M (XY) = M (X) M(Y), kui X ja Y on sõltumatud.

Juhusliku muutuja väärtuste hajumise astet selle keskmise väärtuse ümber hinnata M(X)= A mõisteid tutvustatakse dispersioonidD(X) ja keskmine ruut (standard) hälve. Dispersioon nimetatakse erinevuse ruudu matemaatiliseks ootuseks (X-), need. :

D(X) = M(X- ) 2 = p i ,

Kus =M(X); on defineeritud kui dispersiooni ruutjuur, st. .

Dispersiooni arvutamiseks kasutage valemit:

(4.6)

Dispersiooni ja standardhälbe omadused:

1) D(C)=0, kus C=konst

2) D(CX) = C 2 D(X), (CX) = çCç (X) (4,7)

3) D(X+Y) =D(X)+D(Y),

kui X ja Y on sõltumatud.

Suuruste ja suurus langeb kokku juhusliku suuruse X enda mõõtmega ning D(X) mõõde on võrdne juhusliku suuruse X mõõtme ruuduga.

4.3. Matemaatilised tehted juhuslike suurustega.

Olgu juhusliku suuruse X väärtused tõenäosustega ja juhuslikul suurusel Y väärtused tõenäosustega. Juhusliku suuruse X ja konstantse väärtuse K korrutis KX on uus juhuslik suurus, mis samade tõenäosustega kui juhuslik muutuja X võtab väärtused, mis on võrdsed juhusliku suuruse X K väärtuste korrutistega. Järelikult on selle jaotusseadus kujul Tabel 4.2:

Tabel 4.2

			...
			...

Ruut juhuslik suurus X, st. , on uus juhuslik suurus, mis samade tõenäosustega nagu juhuslik suurus X võtab väärtused, mis on võrdsed selle väärtuste ruutudega.

Summa juhuslikud muutujad X ja Y on uus juhuslik muutuja, mis võtab kõik kuju väärtused tõenäosustega, mis väljendavad tõenäosust, et juhuslik suurus X võtab väärtuse ja Y on väärtus, st

(4.8)

Kui juhuslikud suurused X ja Y on sõltumatud, siis:

Juhuslike suuruste X ja Y erinevus ja korrutis määratakse sarnaselt.

Erinevus juhuslikud muutujad X ja Y - see on uus juhuslik muutuja, mis võtab kõik väärtused kujul ja tööd- kõik vormi väärtused tõenäosustega, mis on määratud valemiga (4.8) ja kui juhuslikud suurused X ja Y on sõltumatud, siis valemiga (4.9).

4.4. Bernoulli ja Poissoni distributsioonid.

Vaatleme n identset korduvat katset, mis vastavad järgmistele tingimustele:

1. Igal testil on kaks tulemust, mida nimetatakse eduks ja ebaõnnestumiseks.

Need kaks tulemust on omavahel kokkusobimatud ja vastandlikud sündmused.

2. Edu tõenäosus, mida tähistatakse p-ga, jääb katsest katseni konstantseks. Ebaõnnestumise tõenäosust tähistatakse q-ga.

3. Kõik n testid on sõltumatud. See tähendab, et sündmuse toimumise tõenäosus üheski n-st korduvast katsest ei sõltu teiste katsete tulemustest.

Tõenäosus, et n sõltumatus korduvas katses, millest igaühes on sündmuse toimumise tõenäosus võrdne , toimub sündmus täpselt m korda (mis tahes järjestuses), on võrdne

(4.10)

Avaldist (4.10) nimetatakse Bernoulli valemiks.

Sündmuse toimumise tõenäosus:

a) vähem kui m korda,

b) rohkem kui m korda,

c) vähemalt m korda,

d) mitte rohkem kui m korda - leitakse vastavalt valemite järgi:

Binoom on diskreetse juhusliku suuruse X jaotuse seadus – sündmuse esinemiste arv n sõltumatus katses, millest igaühes on sündmuse toimumise tõenäosus võrdne p-ga; võimalike väärtuste tõenäosused X = 0,1,2,..., m,...,n arvutatakse Bernoulli valemi abil (tabel 4.3).

Tabel 4.3

Õnnestuste arv X=m				...	m	...	n
Tõenäosus P				...		...

Kuna valemi (4.10) parem pool tähistab binoomlaienduse üldist liiget, nimetatakse seda jaotusseadust nn. binoom. Juhusliku suuruse X jaoks, mis on jaotatud binoomseaduse järgi, on meil.

Kontrollime, kas dispersiooni ühtlase piiri nõue on täidetud. Kirjutame jaotusseaduse :

Leiame matemaatilise ootuse
:

Leiame dispersiooni
:

See funktsioon suureneb, nii et dispersiooni piirava konstandi arvutamiseks saate arvutada piirangu:

Seega on antud juhuslike suuruste dispersioonid piiramatud, mida oli vaja tõestada.

B) Tšebõševi teoreemi sõnastusest järeldub, et dispersioonide ühtlase piirituse nõue on piisav, kuid mitte vajalik tingimus, mistõttu ei saa väita, et seda teoreemi ei saa antud jadale rakendada.

Sõltumatute juhuslike suuruste jada X 1, X 2, ..., X n, ... on antud jaotusseadusega

D(Xn)=M(Xn2)-2,

pidage meeles, et M(X n) = 0, leiame (arvutused jäetakse lugejale)

Oletame ajutiselt, et n muutub pidevalt (selle eelduse rõhutamiseks tähistame n-ga x) ja uurime ekstreemumi funktsiooni φ(x) = x 2 /2 x-1.

Võrdsustades selle funktsiooni esimese tuletise nulliga, leiame kriitilised punktid x 1 = 0 ja x 2 = ln 2.

Jätame esimese punkti ära, kuna see ei paku huvi (n ei võta väärtust, mis võrdub nulliga); on lihtne näha, et punktides x 2 =2/ln 2 on funktsioonil φ(x) maksimum. Arvestades, et 2/ln 2 ≈ 2,9 ja et N on positiivne täisarv, arvutame arvule 2,9 lähimate täisarvude dispersiooni D(X n)= (n 2 /2 n -1)α 2 (vasakul ja õige), t.e. n = 2 ja n = 3 korral.

Kui n = 2, dispersioon D(X 2) = 2α 2, n = 3 korral dispersioon D(X 3) = 9/4α 2. Ilmselgelt

(9/4)α2 > 2α2.

Seega on suurim võimalik dispersioon (9/4)α 2, s.o. juhuslike suuruste Xn dispersioonid on ühtlaselt piiratud arvuga (9/4)α 2 .

Sõltumatute juhuslike suuruste jada X 1 , X 2 , …, X n , … on antud jaotusseadusega

Kas Tšebõševi teoreem on rakendatav antud jadale?

Kommenteeri. Kuna juhuslikud suurused X on identselt jaotatud ja sõltumatud, võib Khinchini teoreemiga tuttav lugeja piirduda ainult matemaatilise ootuse arvutamisega ja veenduda, et see on täielik.

Kuna juhuslikud suurused Xn on sõltumatud, siis veelgi enam ja paaris sõltumatud, s.t. Tšebõševi teoreemi esimene nõue on täidetud.

Lihtne on leida, et M(X n)=0, st esimene matemaatiliste ootuste lõplikkuse nõue on täidetud.

Jääb üle kontrollida, kas dispersioonide ühtlase piirilisuse nõue on täidetud. Vastavalt valemile

D(Xn)=M(Xn2)-2,

arvestame, et M(X n)=0, leiame

Seega on suurim võimalik dispersioon 2, s.o. juhuslike suuruste X n dispersioonid on ühtlaselt piiratud arvuga 2.

Seega on kõik Tšebõševi teoreemi nõuded täidetud, seetõttu on see teoreem vaadeldavale jadale rakendatav.

Leia tõenäosus, et testi tulemusena saab X väärtus intervallis (0, 1/3) sisalduva väärtuse.

Juhuslik suurus X määratakse kogu Ox-teljel jaotatud funktsiooniga F(x)=1/2+(arctg x)/π. Leia tõenäosus, et testi tulemusena saab X väärtus intervallis (0, 1) sisalduva väärtuse.

Tõenäosus, et X võtab mingi intervallis (a, b) sisalduva väärtuse, on võrdne jaotusfunktsiooni juurdekasvuga sellel intervallil: P(a

P(0< Х <1) = F(1)-F(0) = x =1 - x =0 = 1/4

Juhusliku muutuja X jaotusfunktsioon

Leia tõenäosus, et testi tulemusena saab X väärtus intervallis (-1, 1) sisalduva väärtuse.

Tõenäosus, et X võtab mingi intervallis (a, b) sisalduva väärtuse, on võrdne jaotusfunktsiooni juurdekasvuga sellel intervallil: P(a

P(-1< Х <1) = F(1)-F(-1) = x =-1 – x =1 = 1/3.

Pideva juhusliku suuruse X jaotusfunktsioon (mõne seadme tõrkevaba tööaeg) on ​​võrdne F(x)=1st -x/ T (x≥0). Leidke seadme tõrgeteta töötamise tõenäosus aja x≥T jaoks.

Tõenäosus, et X võtab väärtuse, mis sisaldub intervallis x≥T, on võrdne jaotusfunktsiooni juurdekasvuga sellel intervallil: P(0

P(x≥T) = 1 – P(T

Juhusliku muutuja X määrab jaotusfunktsioon

Leia tõenäosus, et testi tulemusena saab X väärtuse: a) väiksem kui 0,2; b) vähem kui kolm; c) vähemalt kolm; d) vähemalt viis.

a) Kuna x≤2 korral on funktsioon F(x)=0, siis F(0, 2)=0, s.t. P(x< 0, 2)=0;

b) P(X< 3) = F(3) = x =3 = 1.5-1 = 0.5;

c) sündmused X≥3 ja X<3 противоположны, поэтому Р(Х≥3)+Р(Х<3)=1. Отсюда, учитывая, что Р(Х<3)=0.5 [см. п. б.], получим Р(Х≥3) = 1-0.5 = 0.5;

d) vastupidiste sündmuste tõenäosuste summa on võrdne ühega, seega P(X≥5)+P(X)<5)=1. Отсюда, используя условие, в силу которого при х>4 funktsiooni F(x)=1, saame P(X≥5) = 1-P(X<5) = 1-F(5) = 1-1 = 0.

Juhusliku suuruse X määrab jaotusfunktsioon

Leia tõenäosus, et nelja sõltumatu katse tulemusena võtab X väärtus intervallile (0,25, 0,75) kuuluva väärtuse täpselt kolm korda.

Tõenäosus, et X võtab mingi intervallis (a, b) sisalduva väärtuse, on võrdne jaotusfunktsiooni juurdekasvuga sellel intervallil: P(a

P(0,25< X <0.75) = F(0.75)-F(0.25) = 0.5

Seetõttu , või Siit või.

Juhuslik suurus X määratakse kogu Ox-teljel jaotusfunktsiooniga. Leidke võimalik väärtus, mis vastab tingimusele: tõenäosusega võtab juhuslik X testi tulemusel suurema väärtuse

Lahendus. Sündmused ja on vastupidised, seega . Seega,. Sellest ajast.

Jaotusfunktsiooni definitsiooni järgi on .

Seetõttu , või . Siit või.

Diskreetne juhuslik suurus X on antud jaotusseadusega

Seega on nõutaval jaotusfunktsioonil vorm

Diskreetne juhuslik suurus X on antud jaotusseadusega

Leidke jaotusfunktsioon ja joonistage selle graafik.

Arvestades pideva juhusliku suuruse X jaotusfunktsiooni

Leidke jaotustihedus f(x).

Jaotustihedus on võrdne jaotusfunktsiooni esimese tuletisega:

Kui x=0 tuletist ei eksisteeri.

Pidevat juhuslikku suurust X määrab jaotustihedus intervallis ; väljaspool seda intervalli. Leidke tõenäosus, et X võtab intervallile kuuluva väärtuse.

Kasutame valemit. Tingimuste järgi ja. Seega nõutav tõenäosus

Pideva juhusliku suuruse X annab jaotustihedus intervallis ; väljaspool seda intervalli. Leidke tõenäosus, et X võtab intervallile kuuluva väärtuse.

Kasutame valemit. Tingimuste järgi ja . Seega nõutav tõenäosus

Pideva juhusliku suuruse X jaotustihedus vahemikus (-π/2, π/2) on võrdne f(x)=(2/π)*cos2x ; väljaspool seda intervalli f(x)=0. Leidke tõenäosus, et kolmes sõltumatus katses võtab X täpselt kaks korda suurema väärtuse, mis sisaldub intervallis (0, π/4).

Kasutame valemit P(a

P(0

Vastus: π+24π.

fx=0, x≤0cosx juures, 0 juures

Me kasutame valemit

Kui x ≤0, siis f(x)=0, seega

F(x)=-∞00dx=0.

Kui 0

F(x)=-∞00dx+0xcosxdx=sinx.

Kui x≥ π2, siis

F(x)=-∞00dx+0π2cosxdx+π2x0dx=sinx|0π2=1.

Niisiis, vajalik jaotusfunktsioon

Fx=0, x≤0sinx juures, 0 juures π2.

Pideva juhusliku suuruse X jaotustihedus on antud:

Fx=0, x≤0sinx juures, 0 juures π2.

Leidke jaotusfunktsioon F(x).

Me kasutame valemit

Pideva juhusliku suuruse X jaotustihedus määratakse kogu Ox-teljel võrrandiga . Leidke konstantne parameeter C.

.

. (*)

.

Seega

Pideva juhusliku suuruse jaotustihedus määratakse kogu teljel võrrandiga Leia konstantne parameeter C.

Lahendus. Jaotustihedus peab vastama tingimusele. Nõuame, et antud funktsiooni puhul oleks see tingimus täidetud:

.

. (*)

Leiame esmalt määramata integraali:

.

Seejärel arvutame vale integraali:

Seega

Asendades (**) tähega (*), saame lõpuks .

Pideva juhusliku suuruse X jaotustihedus intervallis on võrdne ; väljaspool seda intervalli f(x) = 0. Leia konstantne parameeter C.

.

. (*)

Leiame esmalt määramata integraali:

Seejärel arvutame vale integraali:

(**)

Asendades (**) tähega (*), saame lõpuks .

Pideva juhusliku suuruse X jaotustihedus määratakse intervallis võrrandiga ; väljaspool seda intervalli f(x) = 0. Leia konstantne parameeter C.

Lahendus. Jaotustihedus peab täitma tingimust, kuid kuna f(x) väljaspool intervalli on 0, siis piisab, kui see rahuldab: Nõuame, et antud funktsiooni puhul oleks see tingimus täidetud:

.

. (*)

Leiame esmalt määramata integraali:

Seejärel arvutame vale integraali:

(**)

Asendades (**) tähega (*), saame lõpuks .

Juhuslikku suurust X määrab jaotustihedus ƒ(x) = 2x intervallis (0,1); väljaspool seda intervalli ƒ(x) = 0. Leia väärtuse X matemaatiline ootus.

R otsus. Me kasutame valemit

Asendades a = 0, b = 1, ƒ(x) = 2x, saame

Vastus: 2/3.

Juhuslikku suurust X määrab jaotustihedus ƒ(x) = (1/2)x intervallis (0;2); väljaspool seda intervalli ƒ(x) = 0. Leia väärtuse X matemaatiline ootus.

R otsus. Me kasutame valemit

Asendades a = 0, b = 2, ƒ(x) = (1/2)x, saame

M(X) = = 4/3

Vastus: 4/3.

Juhuslikku suurust X intervallis (–s, s) määrab jaotustihedus

ƒ (x) = ; väljaspool seda intervalli ƒ(x) = 0. Leia väärtuse X matemaatiline ootus.

R otsus. Me kasutame valemit

Asendades a = –с, b = c, ƒ(x) = , saame

Arvestades, et integrand on paaritu ja integratsiooni piirid on algpunkti suhtes sümmeetrilised, järeldame, et integraal on võrdne nulliga. Seetõttu M(X) = 0.

Selle tulemuse saab kohe, kui võtta arvesse, et jaotuskõver on sirge x = 0 suhtes sümmeetriline.

Juhuslikku suurust X intervallis (2, 4) määrab jaotustihedus f(x)=

. Sellest on näha, et x = 3 korral saavutab jaotustihedus maksimumi; seega,. Jaotuskõver on sümmeetriline sirge x=3 suhtes, seega .

Juhuslikku suurust X intervallis (3, 5) määrab jaotustihedus f(x)= ; väljaspool seda intervalli f(x)=0. Leidke X režiim, matemaatiline ootus ja mediaan.

Lahendus. Esitame jaotustiheduse kujul . Sellest on näha, et x = 3 korral saavutab jaotustihedus maksimumi; seega,. Jaotuskõver on sümmeetriline sirge x=4 suhtes, seega .

Juhuslikku suurust X intervallis (-1, 1) määrab jaotustihedus ; väljaspool seda intervalli f(x)=0. Leia: a) mood; b) mediaan X.

JUHUSLIKUD MUUTUVAD

Näide 2.1. Juhuslik väärtus X jaotusfunktsiooni poolt antud

Leidke tõenäosus, et testi tulemusena X võtab väärtusi, mis sisalduvad vahemikus (2,5; 3,6).

Lahendus: X intervallis (2,5; 3,6) saab määrata kahel viisil:

Näide 2.2. Milliste parameetrite väärtustel A Ja IN funktsiooni F(x) = A + Be - x võib olla juhusliku muutuja mittenegatiivsete väärtuste jaotusfunktsioon X.

Lahendus: Kuna kõik juhusliku suuruse võimalikud väärtused X kuuluvad intervalli , siis selleks, et funktsioon oleks jaotusfunktsioon jaoks X, peab vara olema täidetud:

.

Vastus: .

Näide 2.3. Juhusliku suuruse X määrab jaotusfunktsioon

Leidke tõenäosus, et nelja sõltumatu testi tulemusel väärtus X täpselt 3 korda võtab intervallile kuuluva väärtuse (0,25; 0,75).

Lahendus: Väärtuse tabamise tõenäosus X intervallis (0,25; 0,75) leiame valemi abil:

Näide 2.4. Tõenäosus, et pall ühe löögiga korvi tabab, on 0,3. Koostage kolme viskega tabamuste arvu jaotusseadus.

Lahendus: Juhuslik väärtus X– kolme löögiga korvi tabamiste arv – võib võtta järgmisi väärtusi: 0, 1, 2, 3. Tõenäosused, et X

X:

Näide 2.5. Kaks laskurit lasevad igaüks ühe lasu märklauda. Tõenäosus, et esimene laskur seda tabab, on 0,5, teine ​​- 0,4. Koostage sihtmärgi tabamuste arvu jaotusseadus.

Lahendus: Leiame diskreetse juhusliku suuruse jaotuse seaduse X– sihtmärgi tabamuste arv. Olgu sündmuseks esimene laskur, kes tabab märklauda, ​​ja teine ​​laskur tabagu sihtmärki ning on vastavalt nende möödalaskmised.

Koostame SV tõenäosusjaotuse seaduse X:

Näide 2.6. Katsetatakse kolme elementi, mis töötavad üksteisest sõltumatult. Elementide tõrkevaba töö ajal (tundides) on jaotustiheduse funktsioon: esimene: F 1 (t) =1-e- 0,1 t, teiseks: F 2 (t) = 1-e- 0,2 t, kolmandaks: F 3 (t) =1-e- 0,3 t. Leidke tõenäosus, et ajavahemikus 0 kuni 5 tundi: ainult üks element ebaõnnestub; ainult kaks elementi ebaõnnestuvad; kõik kolm elementi ebaõnnestuvad.

Lahendus: Kasutame tõenäosuse genereeriva funktsiooni definitsiooni:

Tõenäosus, et sõltumatutes katsetes, millest esimeses on sündmuse toimumise tõenäosus A võrdne sündmusega , teises jne A ilmub täpselt üks kord, mis on võrdne genereeriva funktsiooni laienduskoefitsiendiga astmetes . Leiame vastavalt esimese, teise ja kolmanda elemendi ebaõnnestumise ja mittetõrke tõenäosused ajavahemikus 0 kuni 5 tundi:

Loome genereeriva funktsiooni:

Koefitsient at on võrdne tõenäosusega, et sündmus A ilmub täpselt kolm korda, see tähendab kõigi kolme elemendi ebaõnnestumise tõenäosust; koefitsient at on võrdne tõenäosusega, et täpselt kaks elementi ebaõnnestuvad; koefitsient at on võrdne tõenäosusega, et ainult üks element ebaõnnestub.

Näide 2.7. Arvestades tõenäosustihedust f(x)juhuslik muutuja X:

Leidke jaotusfunktsioon F(x).

Lahendus: Kasutame valemit:

.

Seega näeb jaotusfunktsioon välja järgmine:

Näide 2.8. Seade koosneb kolmest iseseisvalt töötavast elemendist. Iga elemendi ebaõnnestumise tõenäosus ühes katses on 0,1. Koostage jaotusseadus ebaõnnestunud elementide arvu kohta ühes katses.

Lahendus: Juhuslik väärtus X– ühes katses ebaõnnestunud elementide arv – võib võtta järgmisi väärtusi: 0, 1, 2, 3. Tõenäosused, et X võtab need väärtused, leiame Bernoulli valemi abil:

Seega saame järgmise juhusliku suuruse tõenäosusjaotuse seaduse X:

Näide 2.9. 6-osalises partiis on 4 standardset. Juhuslikult valiti 3 osa. Koostage standardosade arvu jaotusseadus valitud osade hulgas.

Lahendus: Juhuslik väärtus X– standardosade arv valitud osade hulgas – võib võtta järgmisi väärtusi: 1, 2, 3 ja on hüpergeomeetrilise jaotusega. Tõenäosused, et X

Kus -- osade arv partiis;

-- standardosade arv partiis;

– valitud osade arv;

-- standardosade arv valitud hulgast.

.

.

.

Näide 2.10. Juhuslikul suurusel on jaotustihedus

ja ei ole teada, kuid , a ja . Leia ja.

Lahendus: Sel juhul juhuslik suurus X on kolmnurkjaotus (Simpsoni jaotus) vahemikus [ a, b]. Numbrilised omadused X:

Seega . Selle süsteemi lahendamisel saame kaks väärtuste paari: . Kuna vastavalt probleemi tingimustele on meil lõpuks: .

Vastus: .

Näide 2.11. Keskmiselt alla 10% lepingutest maksab kindlustusselts kindlustussummasid seoses kindlustusjuhtumi toimumisega. Arvutage selliste lepingute arvu matemaatiline ootus ja hajumine nelja juhuslikult valitud lepingu vahel.

Lahendus: Matemaatilise ootuse ja dispersiooni saab leida valemite abil:

.

SV võimalikud väärtused (lepingute arv (neljast) kindlustusjuhtumi toimumisega): 0, 1, 2, 3, 4.

Arvutame Bernoulli valemi abil erineva arvu lepingute (neljast), mille eest kindlustussummad maksti, tõenäosused:

.

IC jaotusseeria (kindlustusjuhtumi toimumise lepingute arv) on kujul:

	0,6561	0,2916	0,0486	0,0036	0,0001

Vastus: ,.

Näide 2.12. Viiest roosist kaks on valged. Koostage juhusliku suuruse jaotusseadus, mis väljendab valgete rooside arvu kahe samaaegselt võetud vahel.

Lahendus: Kahest roosist koosnevas valikus võib valget roosi kas puududa või olla üks või kaks valget roosi. Seetõttu juhuslik muutuja X võib võtta väärtusi: 0, 1, 2. Tõenäosused, et X võtab need väärtused, leiame selle valemi abil:

Kus -- rooside arv;

-- valgete rooside arv;

– korraga võetud rooside arv;

-- valgete rooside arv võetud rooside hulgas.

.

.

.

Siis on juhusliku suuruse jaotusseadus järgmine:

Näide 2.13. 15-st kokkupandud seadmest 6 vajavad täiendavat määrimist. Koostage lisamäärimist vajavate ühikute arvu jaotusseadus viie juhuslikult valitud koguarvu hulgast.

Lahendus: Juhuslik väärtus X– täiendavat määrimist vajavate ühikute arv viie valitud hulgast – võib võtta järgmisi väärtusi: 0, 1, 2, 3, 4, 5 ja sellel on hüpergeomeetriline jaotus. Tõenäosused, et X võtab need väärtused, leiame selle valemi abil:

Kus -- kokkupandud üksuste arv;

-- ühikute arv, mis vajavad täiendavat määrimist;

– valitud ühikute arv;

-- täiendavat määrimist vajavate üksuste arv valitud hulgas.

.

.

.

.

.

.

Siis on juhusliku suuruse jaotusseadus järgmine:

Näide 2.14. Remondiks saadud 10 kellast 7 nõuavad mehhanismi üldist puhastamist. Kellad ei ole sorteeritud remondi tüübi järgi. Meister, soovides leida puhastamist vajavaid kellasid, uurib neid ükshaaval ja olles sellised kellad leidnud, lõpetab edasise vaatamise. Leidke vaadatud tundide arvu matemaatiline ootus ja dispersioon.

Lahendus: Juhuslik väärtus X– täiendavat määrimist vajavate seadmete arv viie valitud hulgast – võib võtta järgmisi väärtusi: 1, 2, 3, 4. Tõenäosused, et X võtab need väärtused, leiame selle valemi abil:

.

.

.

.

Siis on juhusliku suuruse jaotusseadus järgmine:

Nüüd arvutame koguse numbrilised omadused:

Vastus: ,.

Näide 2.15. Tellija on unustanud vajaliku telefoninumbri viimase numbri, kuid mäletab, et see on paaritu. Leidke matemaatiline ootus ja dispersioon, mitu korda ta enne soovitud numbrini jõudmist telefoninumbri valib, kui ta valib viimase numbri juhuslikult ja ei vali hiljem valitud numbrit.

Lahendus: Juhuslik suurus võib võtta järgmisi väärtusi: . Kuna abonent ei vali edaspidi valitud numbrit, on nende väärtuste tõenäosused võrdsed.

Koostame juhusliku muutuja jaotusseeria:

	0,2

Arvutame välja valimiskatsete arvu matemaatilise ootuse ja dispersiooni:

Vastus: ,.

Näide 2.16. Iga seeria seadme töökindluse testimise ajal ebaõnnestumise tõenäosus on võrdne lk. Määrake katsetamise korral ebaõnnestunud seadmete arvu matemaatiline ootus N seadmeid.

Lahendus: Diskreetne juhuslik muutuja X on rikkis olevate seadmete arv N sõltumatud testid, millest igaühe ebaõnnestumise tõenäosus on võrdne p, jagatud binoomseaduse järgi. Binoomjaotuse matemaatiline ootus võrdub katsete arvuga, mis on korrutatud ühes katses toimuva sündmuse tõenäosusega:

Näide 2.17. Diskreetne juhuslik suurus X võtab 3 võimalikku väärtust: tõenäosusega ; tõenäosusega ja tõenäosusega. Leidke ja teades, et M( X) = 8.

Lahendus: Kasutame matemaatilise ootuse ja diskreetse juhusliku suuruse jaotusseaduse määratlusi:

Leiame:.

Näide 2.18. Tehnilise kontrolli osakond kontrollib toodete standardsust. Tõenäosus, et toode on standardne, on 0,9. Iga partii sisaldab 5 toodet. Leidke juhusliku suuruse matemaatiline ootus X– partiide arv, millest igaüks sisaldab täpselt 4 standardtoodet, kui kontrollitakse 50 partiid.

Lahendus: Sel juhul on kõik läbiviidud katsed sõltumatud ja tõenäosus, et iga partii sisaldab täpselt 4 standardtoodet, on sama, seetõttu saab matemaatilise ootuse määrata valemiga:

,

kus on osapoolte arv;

Tõenäosus, et partii sisaldab täpselt 4 standardtoodet.

Leiame tõenäosuse Bernoulli valemi abil:

Vastus: .

Näide 2.19. Leidke juhusliku suuruse dispersioon X– sündmuse esinemiste arv A kahes sõltumatus katses, kui sündmuse toimumise tõenäosus nendes katsetes on sama ja on teada, et M(X) = 0,9.

Lahendus: Probleemi saab lahendada kahel viisil.

1) SV võimalikud väärtused X: 0, 1, 2. Bernoulli valemi abil määrame nende sündmuste tõenäosused:

, , .

Siis jaotusseadus X on kujul:

Matemaatilise ootuse definitsioonist määrame tõenäosuse:

Leiame SV dispersiooni X:

.

2) Võite kasutada valemit:

.

Vastus: .

Näide 2.20. Normaalse jaotusega juhusliku suuruse ootus ja standardhälve X võrdub vastavalt 20 ja 5. Leidke tõenäosus, et testi tulemusena X võtab intervallis (15; 25) sisalduva väärtuse.

Lahendus: Tavalise juhusliku muutuja tabamise tõenäosus X lõigul alates kuni väljendatakse Laplace'i funktsiooni kaudu:

Näide 2.21. Antud funktsioon:

Millise parameetri väärtusega C see funktsioon on mingi pideva juhusliku suuruse jaotustihedus X? Leidke juhusliku suuruse matemaatiline ootus ja dispersioon X.

Lahendus: Selleks, et funktsioon oleks mõne juhusliku suuruse jaotustihedus, peab see olema mittenegatiivne ja rahuldama omadust:

.

Seega:

Arvutame matemaatilise ootuse valemi abil:

.

Arvutame dispersiooni järgmise valemi abil:

T on võrdne lk. On vaja leida selle juhusliku suuruse matemaatiline ootus ja dispersioon.

Lahendus: Diskreetse juhusliku suuruse X jaotusseadust - sündmuse esinemiste arvu sõltumatutes katsetes, milles igaühes sündmuse toimumise tõenäosus on võrdne , nimetatakse binoomseks. Binoomjaotuse matemaatiline ootus on võrdne katsete arvu ja sündmuse A toimumise tõenäosuse korrutisega ühes katses:

.

Näide 2.25. Sihtmärki tehakse kolm iseseisvat lasku. Iga löögi tabamise tõenäosus on 0,25. Määrake kolme löögiga tabamuste arvu standardhälve.

Lahendus: Kuna tehakse kolm sõltumatut katset ja sündmuse A (tabamuse) esinemise tõenäosus igas katses on sama, siis eeldame, et diskreetne juhuslik muutuja X – sihtmärgi tabamuste arv – jaotub vastavalt binoomseadus.

Binoomjaotuse dispersioon võrdub katsete arvu ja sündmuse toimumise ja mittetoimumise tõenäosuse korrutisega ühes katses:

Näide 2.26. Keskmine 10 minuti jooksul kindlustusseltsi külastavate klientide arv on kolm. Leidke tõenäosus, et järgmise 5 minuti jooksul saabub vähemalt üks klient.

Keskmine 5 minutiga saabuvate klientide arv: . .

Näide 2.29. Rakenduse ooteaeg protsessori järjekorras järgib eksponentsiaalset jaotusseadust, mille keskmine väärtus on 20 sekundit. Leidke tõenäosus, et järgmine (juhuslik) päring ootab protsessoril kauem kui 35 sekundit.

Lahendus: Selles näites matemaatiline ootus ja tõrkemäär on võrdne .

Seejärel soovitud tõenäosus:

Näide 2.30. 15-liikmeline õpilasrühm peab koosolekut saalis, kus on 20 rida, millest igaühes on 10 istekohta. Iga õpilane võtab saalis koha juhuslikult. Kui suur on tõenäosus, et rea seitsmendal kohal ei ole rohkem kui kolm inimest?

Lahendus:

Näide 2.31.

Seejärel klassikalise tõenäosuse määratluse kohaselt:

Kus -- osade arv partiis;

-- mittestandardsete osade arv partiis;

– valitud osade arv;

-- mittestandardsete osade arv valitud hulgas.

Siis on juhusliku suuruse jaotusseadus järgmine.

Jaotustihedus tõenäosused X helistage funktsioonile f(x)– jaotusfunktsiooni esimene tuletis F(x):

Juhusliku suuruse tõenäosusjaotuse tiheduse mõiste X ei kehti diskreetsete koguste puhul.

Tõenäosuse jaotuse tihedus f(x)– nimetatakse diferentsiaaljaotuse funktsiooniks:

Vara 1. Jaotustihedus on mittenegatiivne suurus:

Vara 2. Jaotustiheduse vale integraal vahemikus kuni on võrdne ühtsusega:

Näide 1.25. Arvestades pideva juhusliku suuruse jaotusfunktsiooni X:

f(x).

Lahendus: Jaotustihedus on võrdne jaotusfunktsiooni esimese tuletisega:

1. Arvestades pideva juhusliku suuruse jaotusfunktsiooni X:

Leidke jaotustihedus.

2. On antud pideva juhusliku suuruse jaotusfunktsioon X:

Leidke jaotustihedus f(x).

1.3. Pideva juhuslikkuse arvkarakteristikud

kogused

Oodatud väärtus pidev juhuslik suurus X, mille võimalikud väärtused kuuluvad kogu teljele Oh, määratakse võrdsusega:

Eeldatakse, et integraal koondub absoluutselt.

a,b), See:

f(x)– juhusliku suuruse jaotustihedus.

Dispersioon pidev juhuslik suurus X, mille võimalikud väärtused kuuluvad kogu teljele, määratakse võrdsusega:

Erijuhtum. Kui juhusliku suuruse väärtused kuuluvad intervalli ( a,b), See:

Tõenäosus, et X võtab väärtusi, mis kuuluvad intervalli ( a,b), määratakse võrdsusega:

.

Näide 1.26. Pidev juhuslik muutuja X

Leidke juhusliku suuruse matemaatiline ootus, dispersioon ja tõenäosus X intervallis (0;0,7).

Lahendus: Juhuslik suurus jaotatakse intervallile (0,1). Määrame pideva juhusliku suuruse jaotustiheduse X:

a) Matemaatiline ootus :

b) dispersioon

V)

Tööülesanded iseseisvaks tööks:

1. Juhuslik muutuja X annab jaotusfunktsioon:

M(x);

b) dispersioon D(x);

X intervalli (2,3).

2. Juhuslik muutuja X

Leia: a) matemaatiline ootus M(x);

b) dispersioon D(x);

c) määrab juhusliku suuruse tabamise tõenäosuse X intervalli (1;1,5).

3. Juhuslik muutuja X saadakse kumulatiivse jaotusfunktsiooniga:

Leia: a) matemaatiline ootus M(x);

b) dispersioon D(x);

c) määrab juhusliku suuruse tabamise tõenäosuse X intervallis

1.4. Pideva juhusliku suuruse jaotuse seadused

1.4.1. Ühtlane jaotus

Pidev juhuslik muutuja X on segmendil ühtlaselt jaotunud [ a,b], kui sellel segmendil on juhusliku suuruse tõenäosusjaotuse tihedus konstantne ja väljaspool seda on võrdne nulliga, st:

Riis. 4.

; ; .

Näide 1.27. Buss teatud marsruudil liigub ühtlaselt 5-minutilise intervalliga. Leidke tõenäosus, et ühtlaselt jaotatud juhuslik suurus X– bussi ooteaeg jääb alla 3 minuti.

Lahendus: Juhuslik väärtus X– ühtlaselt jaotatud intervalli peale.

Tõenäosuse tihedus: .

Selleks, et ooteaeg ei ületaks 3 minutit, peab reisija ilmuma peatusesse 2–5 minuti jooksul pärast eelmise bussi väljumist, s.o. juhuslik väärtus X peab langema intervalli (2;5). See. nõutav tõenäosus:

Tööülesanded iseseisvaks tööks:

1. a) leida juhusliku suuruse matemaatiline ootus Xühtlaselt jaotunud intervallis (2;8);

b) leida juhusliku suuruse dispersioon ja standardhälve X, jaotunud ühtlaselt intervallis (2;8).

2. Elektrikella minutiosuti liigub järsult iga minuti lõpus. Leia tõenäosus, et antud hetkel näitab kell aega, mis erineb tegelikust mitte rohkem kui 20 sekundi võrra.

1.4.2. Eksponentjaotus

Pidev juhuslik muutuja X jaotatakse vastavalt eksponentsiaalseadusele, kui selle tõenäosustihedus on kujul:

kus on eksponentsiaaljaotuse parameeter.

Seega

Riis. 5.

Numbrilised omadused:

Näide 1.28. Juhuslik väärtus X– lambipirni tööaeg – on eksponentsiaalse jaotusega. Määrake tõenäosus, et lambipirni tööaeg on vähemalt 600 tundi, kui keskmine tööaeg on 400 tundi.

Lahendus: Vastavalt ülesande tingimustele juhusliku suuruse matemaatiline ootus X võrdub 400 tunniga, seega:

;

Nõutav tõenäosus, kus

Lõpuks:

Tööülesanded iseseisvaks tööks:

1. Kirjutage eksponentsiaalseaduse tihedus- ja jaotusfunktsioon, kui parameeter .

2. Juhuslik muutuja X

Leidke suuruse matemaatiline ootus ja dispersioon X.

3. Juhuslik muutuja X on antud tõenäosusjaotuse funktsiooniga:

Leidke juhusliku suuruse matemaatiline ootus ja standardhälve.

1.4.3. Normaaljaotus

Tavaline nimetatakse pideva juhusliku suuruse tõenäosusjaotuseks X, mille tihedus on kujul:

Kus A– matemaatiline ootus, – standardhälve X.

Tõenäosus, et X võtab intervallile kuuluva väärtuse:

, Kus

- Laplace'i funktsioon.

Jaotus, mille jaoks ; , st. tõenäosustihedusega nimetatakse standardiks.

Riis. 6.

Tõenäosus, et absoluutväärtus lükatakse tagasi, on väiksem kui positiivne arv:

.

Eelkõige siis, kui a= 0 võrdsus on tõsi:

Näide 1.29. Juhuslik väärtus X normaalselt jaotunud. Standardhälve. Leidke tõenäosus, et juhusliku suuruse kõrvalekalle tema matemaatilisest ootusest absoluutväärtuses on väiksem kui 0,3.

Lahendus: .

Tööülesanded iseseisvaks tööks:

1. Kirjutage juhusliku suuruse normaaljaotuse tõenäosustihedus X, teades seda M(x)= 3, D(x)= 16.

2. Normaaljaotusega juhusliku suuruse ootus ja standardhälve X võrdub vastavalt 20 ja 5. Leidke tõenäosus, et testi tulemusena X võtab intervallis (15;20) sisalduva väärtuse.

3. Juhuslikud mõõtmisvead alluvad normaalseadusele standardhälbe mm ja matemaatilise ootusega a= 0. Leia tõenäosus, et 3 sõltumatust mõõtmisest vähemalt ühe viga ei ületa absoluutväärtuses 4 mm.

4. Teatud ainet kaalutakse ilma süstemaatiliste vigadeta. Juhuslikud kaalumisvead alluvad normaalseadusele standardhälbega r. Leidke tõenäosus, et kaalumine toimub veaga, mis absoluutväärtuses ei ületa 10 g.